Spinpack using FPGA

Idea

• generating Hilbert space and matrix is integer(bit)-operation intensive
• replace "get minimum bitpattern of 160 permutations of 40 bits" (4*(160..6400) x86-clocks by 1 FPGA clock, speedup of ca. 400?)
• Testenvironment: single thread (B_NUM=1), remove x86-tricks (would be extra bitlogic, noSBase=1)
• Speed of Hilbert space generation (see numsymconf()) as simplest testcase (ns.t in output)
• later (on production system) other parts could be FPGA replaced (mainly: Hilbert matrix generation, very similar)
• far aim is to eleminate all bit handling, would eliminate need of storing the matrix (stream from FPGA)

setting up test environment

• N=40 square s=1/2 lattice, k=0 sym., PBC, nd=10 (biggest is nd=20)
• ./configure;make speed_test; edit src/config.h (set CONFIG_NOS1SYM); cd exe;./spin >output; grep ns.t output (for numsymconf speed)
• continued ...

Adaptions for FPGA

• depends from FPGA-SW environment (library or FPGA-C-compiler?)
• src/hilbert.c:ns_thread() called by numsymconf()
• calling b_ifsmallest3(cfg) and cfg=next(cfg)
• should be both go to FPGA and stream out to putl1()
• for first test, putl1() can be removed for simplicity
• 5 code lines of loop will be left
• src/hilbert.c:next(cfg) called by ns_thread()
• not important, but may also be put to FPGA (input stream)
• (nd of N) coding, sample (2 of 5): 00011,00101,00110,01001,01010,...
• 2 lines code, counting+searching+moving bits
• x86 clocks needed? n0=(N over nd) calls, 1..N tests ???
• src/hilbert.c:b_ifsmallest3(cfg,buf) called by ns_thread()
• main routine, try 120 permutations and test if cfg is minimum
• the nu==nd part can be through away for first FPGA tests, IFww too
• serial code is optimized, needs going back to more simple version?
• 9lines for nud-symmetry, 16lines related to permutations+minimum
• x86 clocks needed per loop (time/n0)?
  • optimized comparition (skipping low digits if possible):
  • estimation: ((1..160)*(1..40)=(1..6400)) *(cache_access+comparation+loop_overhead)
  • experiment: 132..860clocks (incl.putl1())
  • old stupid version? see get_symconfig() estimated: 6400*x clocks?
• overall x86-clocks: measured 132..836clocks (depend on nd and CPU)
• reduced simplified spinpack version need for FPGA use?

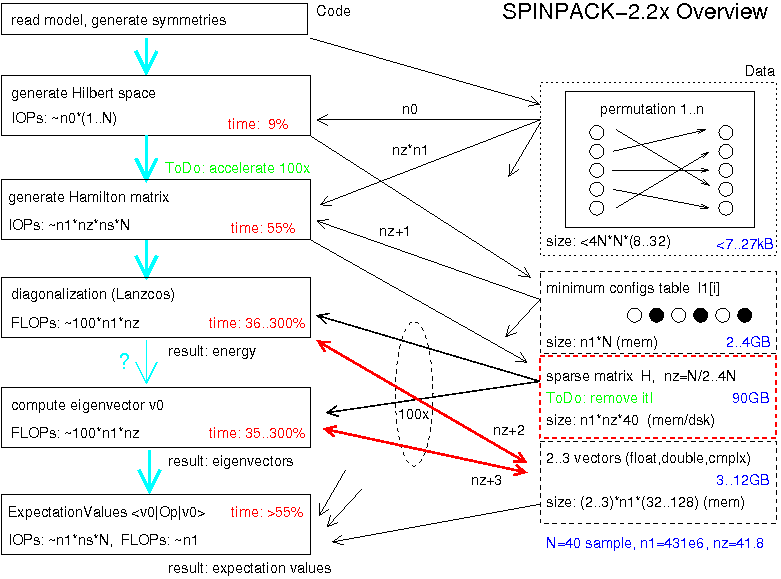
Overview about dataflow

Most data intensive is the sparse matrix (stays in memory or on disk), followed by vectors and config space (stays in memory). Symmetries (permutations) fit into the CPU cache normaly. Matrix is read out sequentially (no latency problem, for big systems its on disk -> bandwith). Space computation is mainly integer or bit driven, but because of missing bit-permutation atomic function its very CPU intensive.

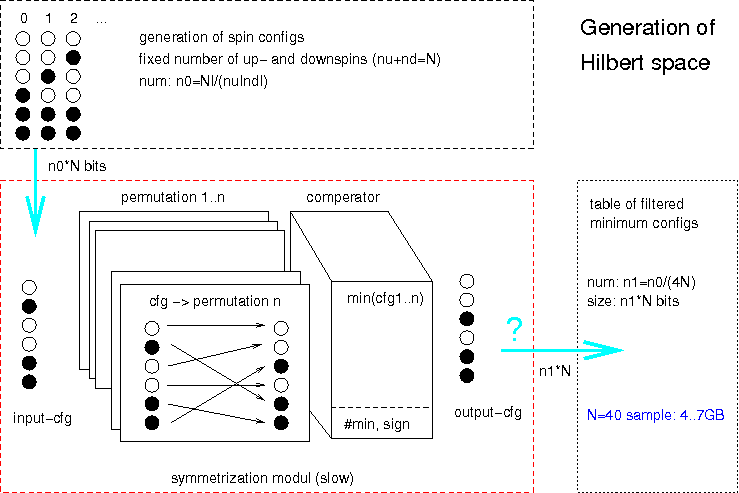
As a first test, space generation could be completely done within FPGA replacing numsymconf() function, writing out minimum symmetric configurations to memory (byte packet or long array).

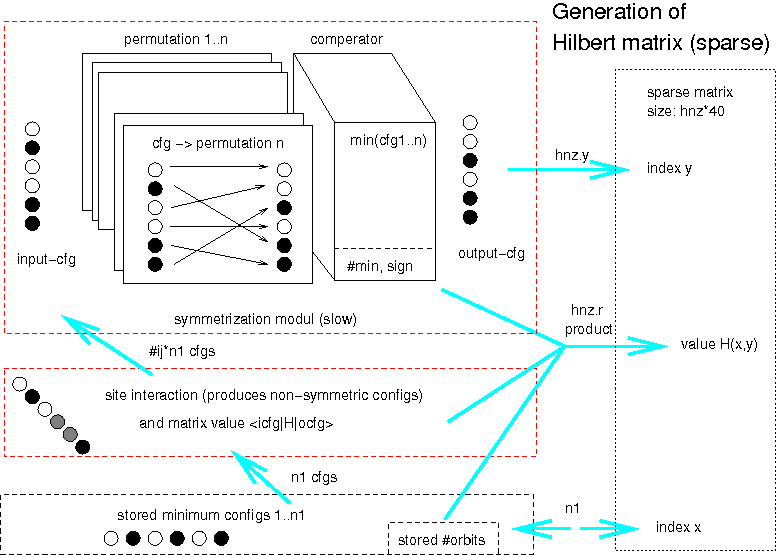
Second test would be implement parts or full hamilton matrix generation to FPGA, if speedup is about 100, matrix could be generated on the fly on every iteration without the need of storing the matrix. This would reduce bandwith problems to disk for bigger spin systems. Nowadays we are limited by disk bandwith (100MB/s) and could go to FPGA streams about 1GB/s per node (speedup 10 without needs of disks and better scaling).

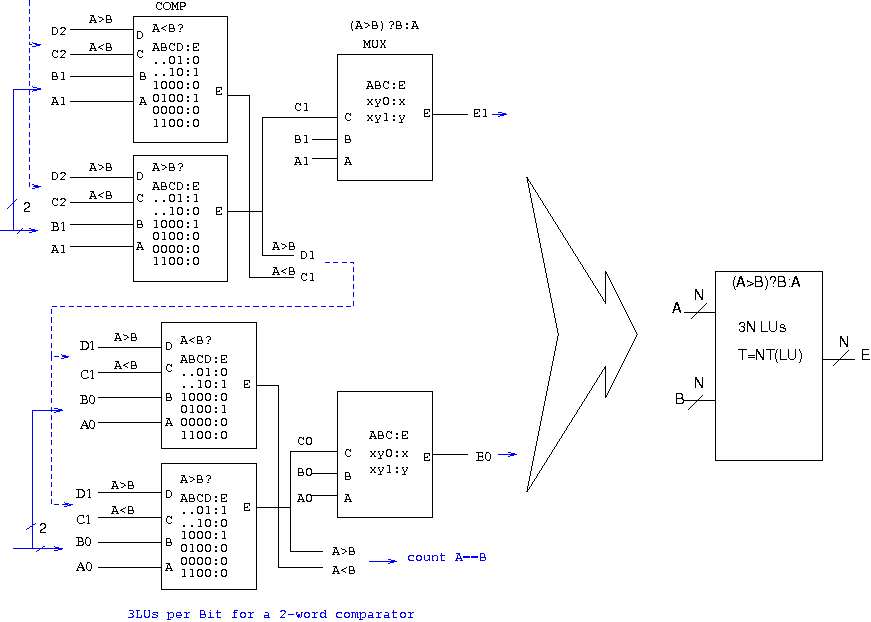
Estimation of FPGA logic needs to compare 40bits configurations to get the minimum. Permutations at zero costs (just wires)?