Stephan Mertens - Research Home | Research | Publications | Teaching | Smorgasbord

Lattice Animals

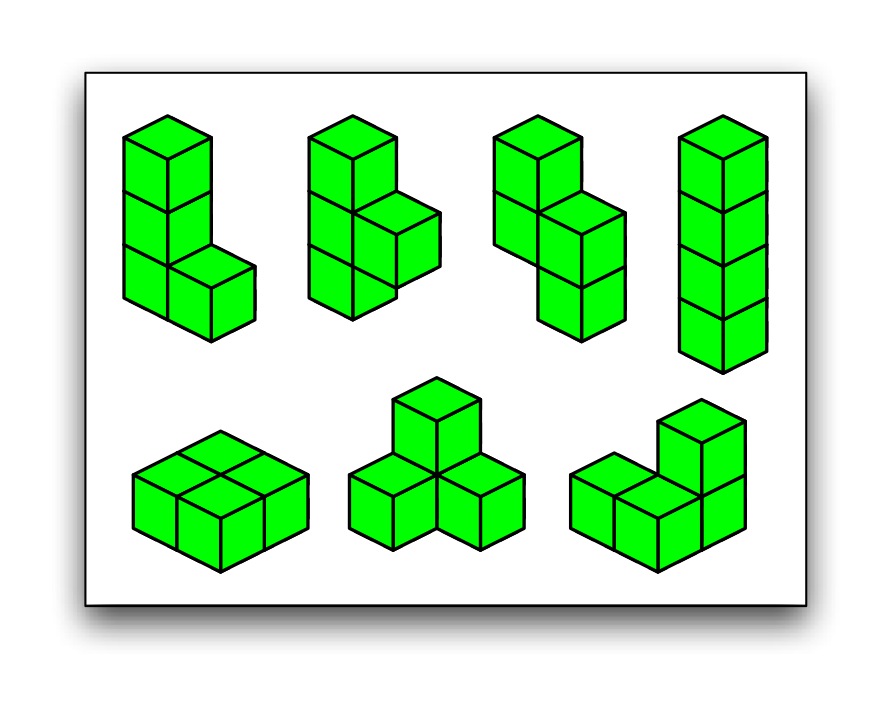
A lattice animal is a finite set of connected vertices of a regular lattice. Lattice animals on the square lattice are better known as polyominoes. On the cubic lattice they are called polycubes. The figure above shows all possible polycubes of size n = 4.

The enumeration of lattice animals is a longstanding combinatorial problem that has some motivations in physics, for example in the study of branched polymers and percolation. For most lattices we don't know a formula for the number of lattice animals of a given size n, and all we can do is to count them one by one. Since the number of lattice animals grows exponentially with n, this counting is a demanding task, even with a fast computer.

We develop fast algorithms for the enumeration of lattice animals, and we run these algorithms on parallel computers. We also work out combinatorial arguments that complement computer based enumerations.

Please check out the publications if you want to learn more about the problem and our algorithms. If you are an expert, you might want to go directly to the enumeration data or to the source code.

Publications

New enumerations and analytical results for the number of bond animals on hypercubic lattices:

• Series expansion of the percolation threshold on hypercubic lattices (with C. Moore)
  Journal of Physics A 51 (2018) 475001

The algorithm and the combinatorial arguments that have been used to compute the data for hypercubic lattices in dimensions d ≥ 3 on this webpage are described in

• The Perimeter of Proper Polycubes (with S. Luther)
  Journal of Integer Sequences 20 (2017) Article 17.9.5
• Counting Lattice Animals in High Dimensions (with S. Luther)
  Journal of Statistical Mechanics: Theory and Experiment 2011 (2011) P09026 /li>

In these older papers we describe the basic algorithm, its efficient and parallel implementation:

• Counting Lattice Animals: A Parallel Attack (with M.E. Lautenbacher)
  Journal of Statistical Physics 66 (1992) 669-678
• Lattice Animals: A Fast Enumeration Algorithm and New Perimeter Polynomials
  Journal of Statistical Physics 58 (1990) 1095-1108

Data

Perimeter Polynomials for Site Animals

The file perimeterpolynomials.tar contains a folder for each dimension d=3..10, each folder contains files "perimeter.n" for the coefficients g_n,t.

The coefficients G_n to compute the formula for the perimeter polynomials for arbitrary dimension d and fixed size n are listed in the following files:

n	2	3	4	5	6	7	8	9	10	11	12
Gn	G2.dat	G3.dat	G4.dat	G5.dat	G6.dat	G7.dat	G8.dat	G9.dat	G10.dat	G11.dat	G12.dat

Perimeter Polynomials for Bond Animals

The file gd_bond.dat contains the number of bond animals in dimension d of size e, perimeter t and number of vertices v.

e	2	3	4	5	6	7	8	9	10	11
gg	g2_bond.dat	g3_bond.dat	g4_bond.dat	g5_bond.dat	g6_bond.dat	g7_bond.dat	g8_bond.dat	g9_bond.dat	g10_bond.dat	g11_bond.dat

The coefficients G_e,t,v to compute the formulas for the perimeter polynomials for arbitrary dimension d and fixed size e are listed in the following files:

e	2	3	4	5	6	7	8	9	10	11
Ge	G2_bond.dat	G3_bond.dat	G4_bond.dat	G5_bond.dat	G6_bond.dat	G7_bond.dat	G8_bond.dat	G9_bond.dat	G10_bond.dat	G11_bond.dat

Cluster Numbers and Series Expansions for Site Animals

The file Ad_poly.txt contains the polynomials to compute the number A_d(n) for given size n and arbitrary dimension d. We know these formulas up to n=14.

cluster numbers Ad(n)			cluster series Sd
d	data	OEIS	data	OEIS
3	A3.dat	A001931	S3.dat	A003211
4	A4.dat	A151830	S4.dat
5	A5.dat	A151831	S5.dat
6	A6.dat	A151832	S6.dat
7	A7.dat	A151833	S7.dat
8	A8.dat	A151834	S8.dat
9	A9.dat	A151835	S9.dat
10	A10.dat		S10.dat

Source Code

Python scripts to compute G_n,t^n-1 and G_n,t^n-2, the number of polycubes (lattice animals) of size n and perimeter t, that are proper in dimension n-1 or dimension n-2.

• proper.tar contains Python scripts G1.py, G2.py and proper.py (code shared by G1.py and G2.py)

Redelemeier's algorithm for the enumeration of bond- and site-animals in hypercubic lattices:

• redelmeier.tar

See README for details, how to compile and use the software (including parallelization on distributed or shared memory computers).