Stephan Mertens - Research Home | Research | Publications | Teaching | Smorgasbord

The Number Partioning Problem

Note: If you are interested in the Number Partitioning Problem you should consider to read Brian Hayes' nice article “The easiest hard problem“ in the American Scientist issue of March-April 2002 or my own review.

The number partitioning problem (NPP) is defined as follows: Given a set of n non-negative, integer numbers a[1],a[2],...,a[n], divide this set into two subsets such that the sums of the numbers in each subset are as nearly equal as possible.

Partitioning is of both theoretical and practical importance. It is one of Garey and Johnson's six basic NP-complete problems that lie at the heart of the theory of NP-completeness. Among the many practical applications one finds multiprocessor scheduling and the minimization of VLSI circuit size and delay.

The analysis of the number partitioning problem is a nice example of the emerging field of experimental mathematics.

NPP displays a phase transition in its computational complexity: As long as N is smaller than the number of bits needed to encode the a[]'s, the computational costs grow exponentially with N. If N exceeds this value, the computational costs decrease dramatically, and for even larger values, the costs grow again, but only linearly. Here is an example for the task to partition 25-bit integers:

Details and a description of the algorithm can be found here.

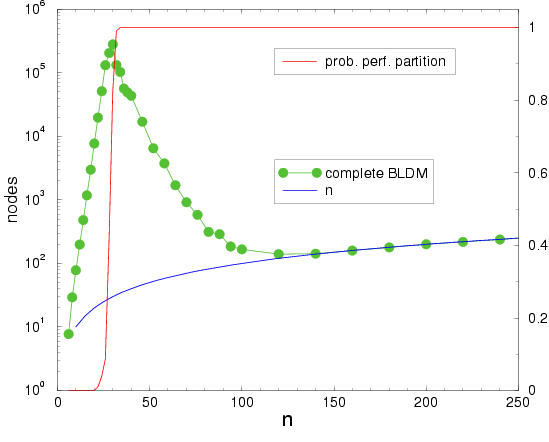
The NPP can be mapped onto an infinite range, antiferromagnetic Mattis spin-glass. An analysis of the statistical mechanics of this model yields accurate quantitative results on the phase transition, like the order parameter and its critical value, and the average value of the optimum solution. Details of this approach ca be found here.

A even simpler analysis is based on the observation that the NPP can be mapped onto a random energy model. This approach allows the calculation of the probability densities of the optimum solution, the second best solution and so on.

Both examples show, that in contrast to most combinatorial optimization problems, the statistical mechanics approach to the NPP is surprisingly simple and yields exact results. Hence the NPP is well suited as a textbook example to introduce some of the basic notions and techniques that statistical physics offers to combinatorial optimization.